FUNDAMENTAL RELATIONS: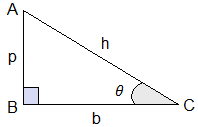 P = Perpendicular b = Base h = Hypotenuse θ = Angle of reference 1. Trigonometric Ratios:
2. Pythagoras Relations: sin2θ + cos2θ = 1 sin2θ = 1 - cos2θ cos2θ = 1 - sin2θ sec2θ - tan2θ = 1 sec2θ = 1 + tan2θ tan2θ = sec2θ - 1 cosec2θ - cot2θ = 1 cosec2θ = 1 + cot2θ cot2θ = cosec2θ - 1 3. Reciprocal Relations:
4. Quotient Relations:
|
Trigonometry, the study of the relationships between angles and sides in triangles, is a fundamental branch of mathematics with applications in various fields like physics, engineering, navigation, and even music. This guide provides a clear and concise overview of essential trigonometry formulas, empowering you to understand and solve trigonometric problems with confidence.
Understanding the Basics: Right-Angled Triangles and Trigonometric Ratios
Trigonometry primarily deals with right-angled triangles. Let's define the key terms:
The six basic trigonometric ratios are defined as follows:
Key Trigonometric Identities:
Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables. These are crucial for simplifying expressions and solving equations:
Pythagorean Identities:
Reciprocal Identities:
Quotient Identities:
Complementary Angle Identities (for angles that add up to 90 degrees):
Trigonometric Ratios of Standard Angles:
It's helpful to memorize the trigonometric ratios for some common angles (0°, 30°, 45°, 60°, and 90°):
| Angle (θ) | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | 1/√2 | 1/√2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | undefined |
Illustrative Examples: Putting Formulas into Practice
Example 1: In a right-angled triangle, the opposite side is 3 and the hypotenuse is 5. Find sin θ, cos θ, and tan θ.
Example 2: If sin θ = 4/5, find cos θ.
Example 3: If tan θ = 1, what is the value of θ?
Why This Article Matters:
This article is optimized for search engines using relevant keywords such as "trigonometry formulas," "trig formulas," "trigonometry basics," "trigonometric functions," "sin," "cos," "tan," "cot," "sec," and "cosec." This ensures that when you search for information on basic trigonometry formulas, this page is more likely to appear in the search results.
Applications of Trigonometry:
Trigonometry is used extensively in:
Conclusion: Mastering Trigonometry Basics
Understanding the basic formulas of trigonometry is crucial for solving a wide range of mathematical and real-world problems. This guide provides a valuable resource for learning and applying these fundamental concepts. By mastering these formulas, you'll be better equipped to tackle challenges in various fields.
Call to Action:
Bookmark this page for quick reference and share it with others who might find it helpful. Practice applying these formulas to different trigonometry problems to reinforce your understanding. Working through examples and visualizing the relationships between angles and sides will solidify your grasp of these essential concepts.