| 1. | For Any Triangle ABC: In terms of base(b) and height(h),
In terms of three sides a, b, c,
Perimeter = a+b+c | 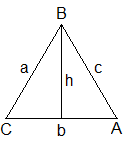 | ||||||||||
| 2. | For Right Angled Triangle ABC: p = perpendicular (AB) b = base (BC) h = hypotenuse(AC)
Perimeter = p+b+h |  | ||||||||||
| 3. | For Equilateral Triangle ABC: a = side of equilateral triangle
Perimeter = 3a |  | ||||||||||
| 4. | For Isosceles Triangle ABC: a = two equal sides (AB and AC) b = base (BC)
Perimeter = 2a+b |  |
Triangles are fundamental geometric shapes that appear everywhere, from the simplest structures to the most complex designs. Understanding their properties and mastering the formulas for calculating their area, perimeter, and other key measurements is essential for various fields, including mathematics, engineering, and architecture. This guide provides a clear and concise overview of triangle mensuration formulas, empowering you to solve triangle-related problems with ease.
Understanding Triangle Basics: Sides, Angles, and Types
Before diving into the formulas, let's recap the basic properties of triangles:
Essential Triangle Mensuration Formulas:
Here's a breakdown of the key formulas you'll need:
Area of a Triangle (using base and height):
Area of a Triangle (using Heron's formula - when all sides are known):
Area of an Equilateral Triangle:
Perimeter of a Triangle:
Perimeter of an Equilateral Triangle:
Height of a Triangle (when area and base are known):
Pythagorean Theorem (for Right Triangles only):
Illustrative Examples: Putting Formulas into Practice
Let's work through some examples to understand how to apply these formulas:
Example 1: A triangle has a base of 10 cm and a height of 8 cm. Calculate its area.
Example 2: An equilateral triangle has a side length of 6 cm. Calculate its area.
Example 3: A triangle has sides of length 3 cm, 4 cm, and 5 cm. Calculate its area using Heron's formula.
Example 4: A right triangle has legs of length 5 cm and 12 cm. Calculate the length of the hypotenuse.
Why This Article Matters:
This article is optimized for search engines using relevant keywords such as "triangle mensuration formulas," "triangle area," "triangle perimeter," "base and height formula," "triangle calculations," "geometry formulas," "math formulas," and "triangle properties." This ensures that when you search for information on triangle mensuration, this page is more likely to appear in the search results.
Applications of Triangle Mensuration:
Triangle mensuration has applications in various fields, including:
Conclusion: Mastering Triangle Mensuration
Understanding triangle mensuration is essential for solving a wide range of geometric problems. This guide provides a valuable resource for learning and applying these fundamental formulas. By mastering these concepts, you'll be better equipped to tackle challenges in mathematics, science, and engineering.
Call to Action:
Bookmark this page for quick reference and share it with others who might find it helpful. Practice applying these formulas to different triangle problems to reinforce your understanding. The more you work with these concepts, the more confident you'll become in solving triangle-related challenges.