Mensuration: Cylinder Formula

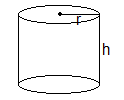Cylinders are ubiquitous three-dimensional shapes, found in everything from cans and pipes to tanks and rollers. Understanding their properties and mastering the formulas for calculating their surface area, volume, and other key measurements is essential for various fields, including mathematics, engineering, and design. This comprehensive guide provides a clear and concise overview of cylinder mensuration formulas, empowering you to solve 3D geometry problems with confidence.

Understanding Cylinders: Key Properties

Before diving into the formulas, let's define the key characteristics of cylinders:

• Shape: A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface.
• Bases: The two circular faces are congruent and parallel.
• Curved Surface: The curved surface connects the two circular bases.
• Radius (r): The radius of the circular bases.
• Height (h): The perpendicular distance between the two circular bases.

Essential Cylinder Mensuration Formulas:

Here's a breakdown of the key formulas you'll need:

• Volume (V): V = πr²h
• Curved Surface Area (CSA) or Lateral Surface Area (LSA): CSA = 2πrh
• Total Surface Area (TSA): TSA = CSA + 2 * (Area of circular base) or TSA = 2πrh + 2πr²

Formulas Related to Radius and Diameter:

• Diameter (d): d = 2r
• Radius (r): r = d/2

Illustrative Examples: Putting Formulas into Practice

Let's work through some examples to understand how to apply these formulas:

• Example 1: A cylinder has a radius of 5 cm and a height of 10 cm. Calculate its volume and curved surface area.

  • Volume = π * (5 cm)² * 10 cm = 250π cm³ ≈ 785.40 cm³
  • CSA = 2 * π * 5 cm * 10 cm = 100π cm² ≈ 314.16 cm²

• Example 2: A cylindrical water tank has a diameter of 2 meters and a height of 3 meters. Calculate its volume and total surface area.

  • Radius = 2 m / 2 = 1 m
  • Volume = π * (1 m)² * 3 m = 3π m³ ≈ 9.42 m³
  • TSA = 2π * 1 m * 3 m + 2π * (1 m)² = 8π m² ≈ 25.13 m²

• Example 3: A cylindrical can has a radius of 4cm and a height of 12cm. Find its total surface area.

  • TSA = 2π * 4 * 12 + 2π * 4² = 96π + 32π = 128π cm² ≈ 402.12 cm²

Why This Article Matters:

This article is optimized for search engines using relevant keywords such as "cylinder formulas," "surface area," "volume formula," "radius formula," "height formula," "3D geometry," "geometry formulas," "math formulas," and "cylinder calculations." This ensures that when you search for information on cylinder mensuration, this page is more likely to appear in the search results.

Applications of Cylinder Mensuration:

Cylinder mensuration has applications in various fields, including:

• Engineering: Calculating the volume and surface area of pipes, tanks, and other cylindrical components.
• Construction: Determining the amount of material needed for cylindrical structures.
• Manufacturing: Designing cylindrical containers and packaging.
• Physics: Studying fluid flow and pressure in cylindrical pipes.
• Everyday life: Calculating the capacity of cylindrical containers, the amount of paint needed for a cylindrical surface, etc.

Conclusion: Mastering Cylinder Mensuration

Understanding cylinder mensuration is essential for solving a wide range of 3D geometry problems. This guide provides a valuable resource for learning and applying these fundamental formulas. By mastering these concepts, you'll be better equipped to tackle challenges in mathematics, science, engineering, and various real-world applications.

Call to Action:

Bookmark this page for quick reference and share it with others who might find it helpful. Practice applying these formulas to different cylinder problems to reinforce your understanding. Visualizing these shapes and working through examples will solidify your grasp of cylinder mensuration.